1. Scopo e obiettivi
1.1 Generalità
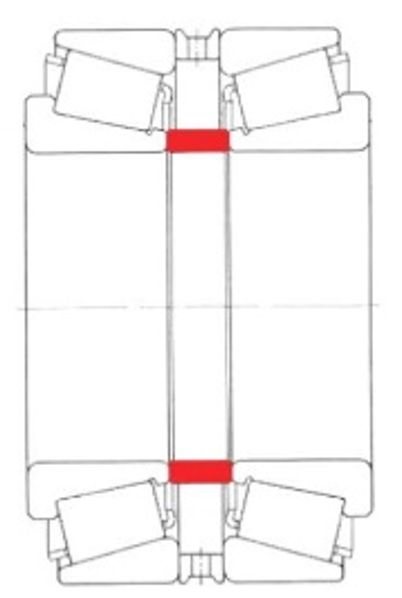
Figura 1
Nella pratica esistono diversi metodi per accoppiare e precaricare i cuscinetti a rulli conici: back-to-back (disposizione O), face-to-face (disposizione X), tandem (per l’aumento della capacità di carico assiale), nonché accoppiamenti con gioco, con precarico rigido o con precarico a molla. Nel caso di set accoppiati in fabbrica (set duplex), il precarico oppure il gioco assiale sono predefiniti mediante anelli distanziatori forniti a corredo.
L’accoppiamento di cuscinetti non selezionati e accoppiati in fabbrica richiede invece un maggiore impegno: una misurazione preliminare delle dimensioni assiali effettive rilevanti dei cuscinetti e dell’alloggiamento, la definizione dei valori obiettivo del gioco assiale e – nel caso della disposizione O – oltre a un distanziale esterno, anche la realizzazione di un anello di regolazione interno, rettificato con sufficiente precisione (figura 1), in conformità ai requisiti derivanti dalle condizioni di impiego.
1.2 Principio di precarico
Qualora una coppia di cuscinetti a rulli conici con precarico specifico, in disposizione O rigida, debba essere supportata tramite l’alloggiamento, per il calcolo della lunghezza effettiva del distanziale è necessario rilevare anche la larghezza dell’alloggiamento (HW) (figura 2). La rappresentazione considera esclusivamente le distanze geometriche nominali e non tiene conto di effetti fisici quali dilatazioni termiche o influenze dovute alle tolleranze di accoppiamento.
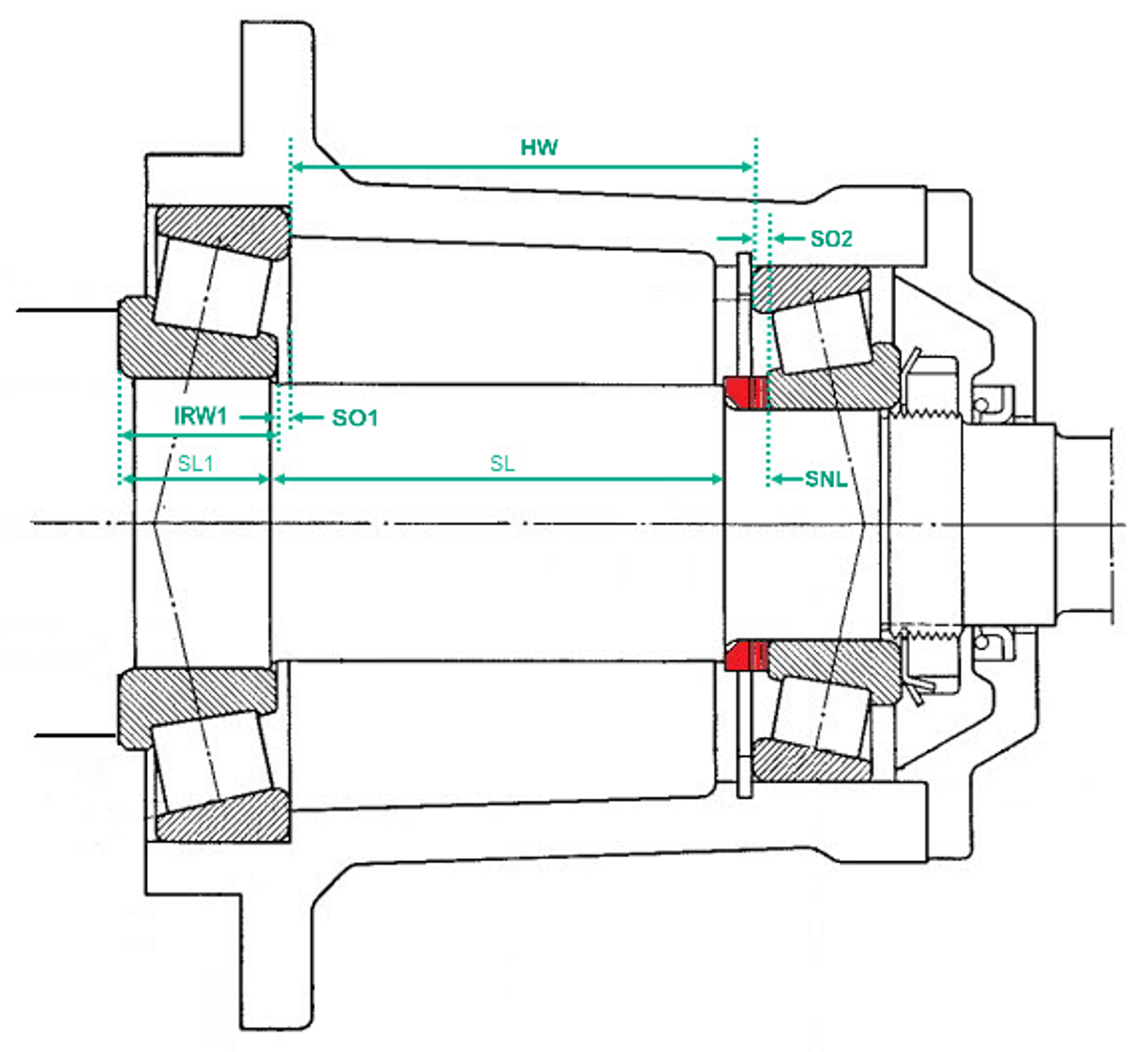
Figura 2
Le sporgenze delle facciate misurate (figura 3), insieme alla larghezza dell’alloggiamento (HW), sono utilizzate per determinare la distanza assiale interna tra i due cuscinetti.
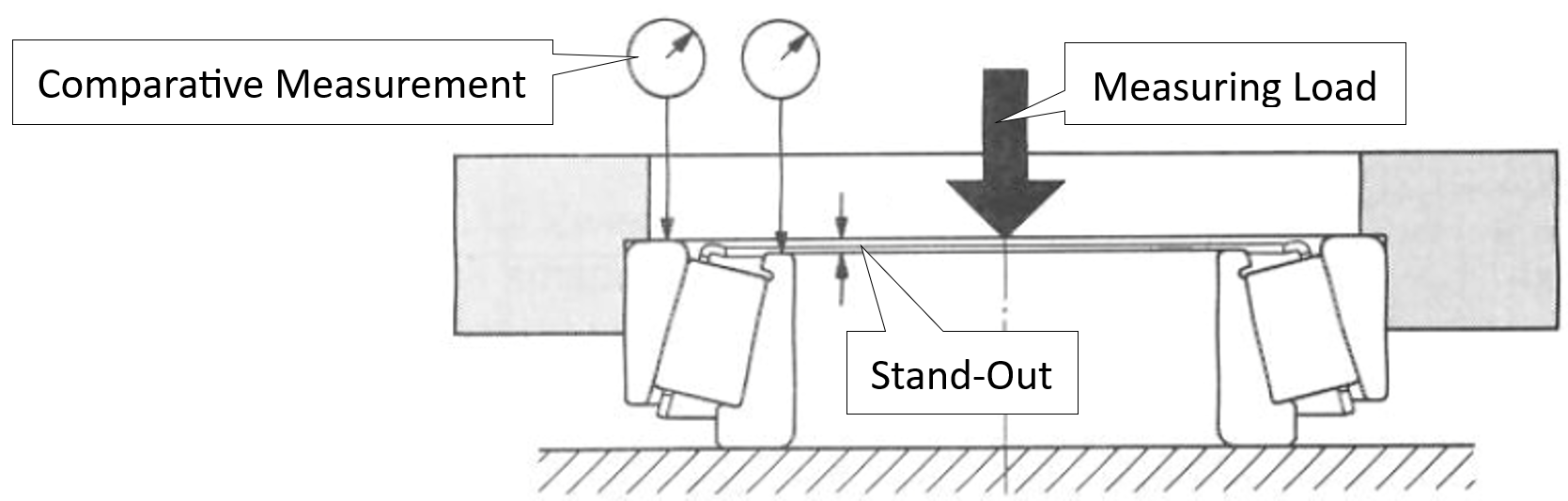
Figura 3
In tal modo è possibile determinare anche la lunghezza nominale del distanziale (SNL) come segue: SNL = (HW) + sporgenze (SO1 & 2) + larghezza dell’anello interno 1 (IRW1) − lunghezze dei segmenti d’albero (SL1 & SL).
SNL = HW + SO1 + SO2 + IRW – (SL1+ SL)
La riduzione assiale del distanziale da definire corrisponde, tenendo conto degli effetti dinamici, termici e fisici, allo spostamento di precarico della coppia di cuscinetti a rulli conici. Tali influenze possono essere determinate in modo analitico ed efficiente con MESYS.
1.3 Esempio applicativo
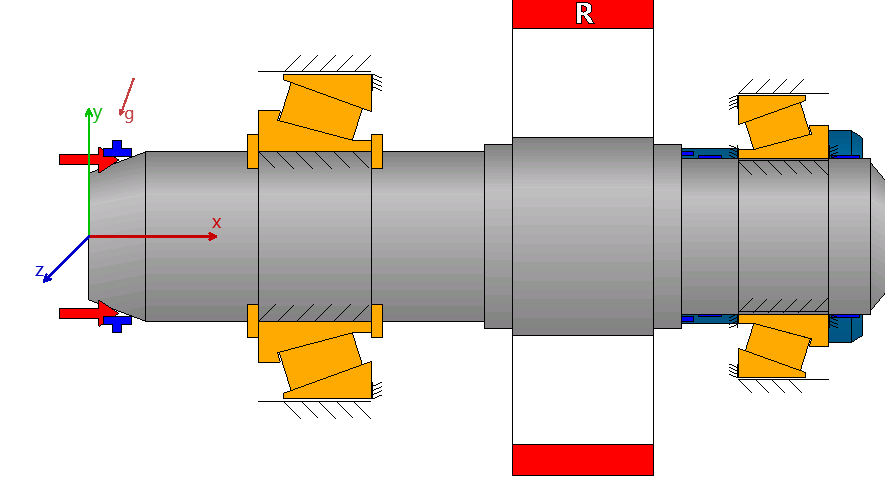
Figura 4
Il presente documento illustra la progettazione di una coppia di cuscinetti a rulli conici con precarico rigido in disposizione O, per il supporto dell’albero di uscita di un riduttore in un’applicazione navale. L’obiettivo è determinare direttamente il precarico necessario dei cuscinetti mediante il Calcolo dell’Albero MESYS, tenendo conto di tutte le influenze misurabili derivanti da una condizione di esercizio definita. Un precarico adeguato dei cuscinetti viene definito mediante la specifica dello spostamento di precarico.
Esso viene realizzato, da un lato, tramite il distanziale e, dall’altro, mediante la forza di serraggio necessaria generata dal ghiera dell’albero.
1.4 Contesto e particolarità dell’applicazione
Vengono considerati i casi di carico più probabili, quali la spinta del propulsore in marcia avanti (ahead) e in retromarcia (astern). Le forze risultanti dell’ingranamento elicoidale confluiscono nel modello di carico come componenti tangenziali, radiali e assiali.

Figura 5
Le condizioni ambientali – lubrificazione a olio, differenze di temperatura tra albero e alloggiamento, nonché interferenze di montaggio e di accoppiamento (IR/OR) – vengono prese in considerazione.
Poiché nel tempo la spinta in marcia avanti risulta predominante, vengono impiegati cuscinetti di dimensioni differenti.
1.5 Attuazione degli obiettivi e strategia di verifica
La progettazione deve garantire, per quanto non in contrasto con altri vincoli al contorno, una forza minima sul cuscinetto in ogni condizione operativa. Devono essere esclusi stati di slittamento – in particolare in presenza di forti variazioni di carico – nonché il conseguente sollevamento (lift-off) dei rulli. Il correlato aumento della temperatura dovuto alla maggiore forza di base derivante dal precarico è ritenuto accettabile in presenza di lubrificazione a olio.
La durata di vita viene verificata mediante uno spettro di carico trasparente. A tal fine, i quattro stati di esercizio STOP, IDLE, AHEAD e ASTERN vengono considerati ciascuno con un rapporto di trasmissione fisso, ponderati con quote temporali ipotetiche e condensati in un carico equivalente sul cuscinetto. Su questa base viene verificato un intervallo di revisione di 7 anni oppure una vita di riferimento modificata di almeno 11’200 h.
La corretta forza di serraggio della ghiera deve essere derivata dalle forze contributive. Il punto di partenza è la forza necessaria allo spostamento degli anelli in presenza di interferenza con l’albero o con l’alloggiamento. A questa si aggiunge la forza di precarico risultante della coppia di cuscinetti. Infine, deve essere considerata una forza di serraggio aggiuntiva della ghiera, destinata a compensare le variazioni dovute ai carichi dinamici sull’insieme di montaggio. Dalla somma dei contributi di forza risulta la forza di serraggio da impostare oppure, qui non ulteriormente trattata, la coppia di serraggio della ghiera ad essa associata.
La robustezza della progettazione del precarico deve essere dimostrata mediante la parametrizzazione delle posizioni di tolleranza di accoppiamento e assumendo i gradienti termici che ne derivano, considerando un carico equivalente singolare coerente con lo spettro di carico e riferito alla vita utile del sistema.
2. Contesto iniziale
2.1 Concetto di propulsione
L’applicazione ipotetica analizzata rappresenta l’albero di uscita di un riduttore marino. Per la spinta in marcia avanti di 25 kN (ahead) viene assunto un momento torcente applicato di 2 500 Nm, mentre per la spinta in retromarcia (astern) viene considerato un momento di 1 500 Nm – in entrambi i casi a una velocità di rotazione costante di 1 600 rpm.
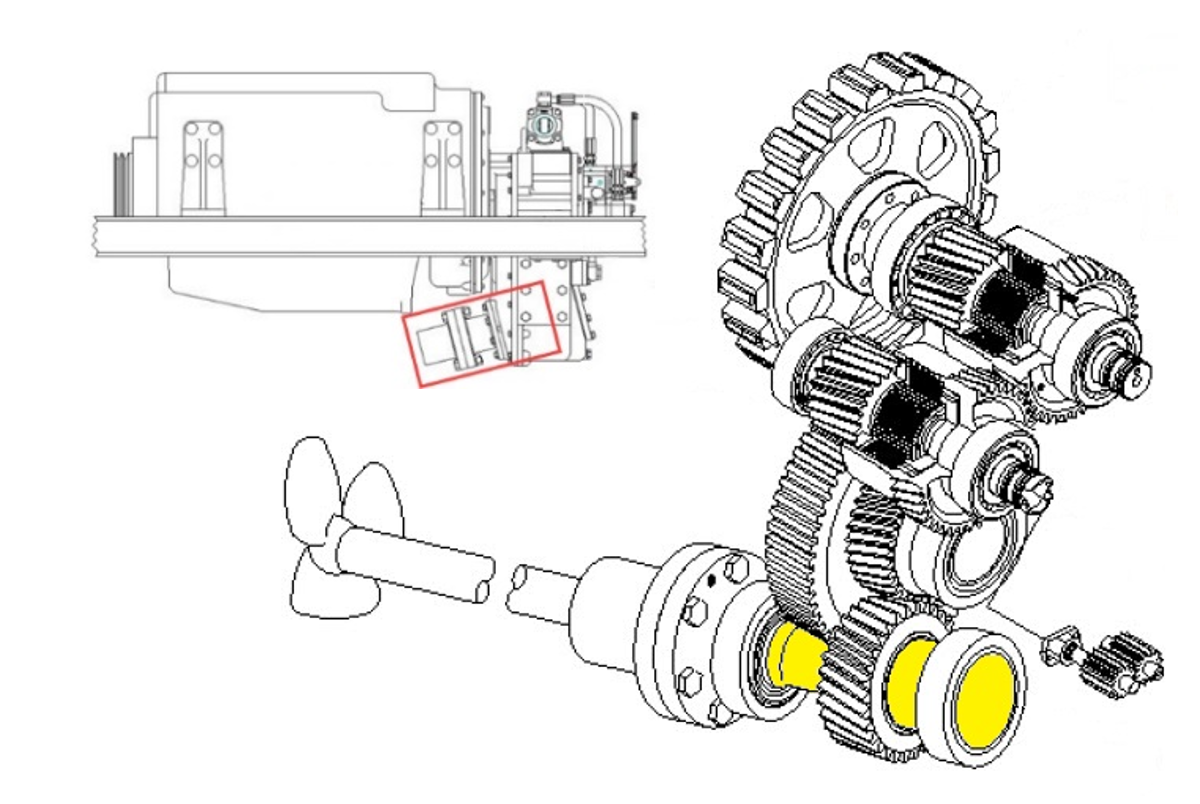
Figura 6
Le forze di spinta corrispondenti vengono derivate senza una progettazione dettagliata dell’elica, mediante l’approccio formale Open Water. A tal fine vengono utilizzati i coefficienti adimensionali dell’elica KT (spinta) e KQ (coppia).
Tprop = KT/KQ * Q/D
A diametro dell’elica D fissato e con un rapporto KT/KQ costante nel punto di funzionamento considerato, la spinta risulta proporzionale alla coppia sull’albero Q. In tal modo i livelli di spinta possono essere derivati in modo coerente dai valori di coppia.
2.2 Ingranaggio cilindrico elicoidale
Per la trasmissione della potenza viene impiegato un ingranaggio cilindrico con angolo d’elica di 20° e con ulteriori caratteristiche, riportate in figura 7:
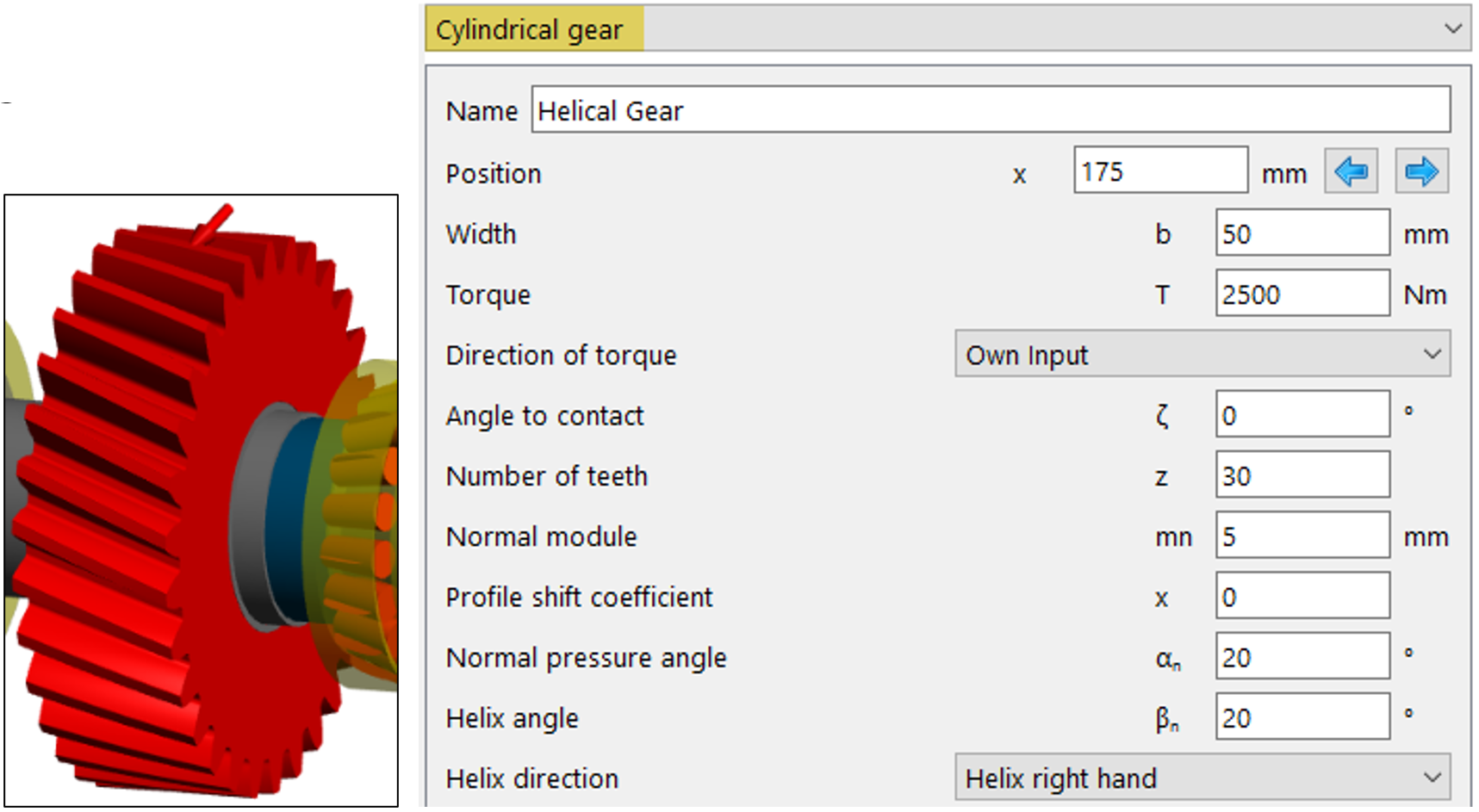
Figura 7
2.3 Concetto di supporto dei cuscinetti
L’albero pieno con ingranaggio montato è supportato da due cuscinetti a rulli conici in una disposizione O (back-to-back) con precarico rigido.
Vengono adottate le seguenti configurazioni di ingranaggio e cuscinetti:
– Ingranaggio con b = 50 mm; z = 30; mn = 5; angolo d’elica βn = 20°
– Outboard: 60 × 115 × 40 con angolo di contatto 20°; C = 156,064 kN, C0 = 211,631 kN
– Inboard: 55 × 100 × 32 con angolo di contatto 19,8°; C = 111,023 kN, C0 = 147,668 kN
La disposizione O offre un’elevata rigidezza al ribaltamento e un supporto univoco delle forze assiali in entrambe le direzioni; il cuscinetto outboard, di dimensioni maggiori e con angolo di contatto di 20°, è dimensionato per assorbire la spinta dominante in marcia avanti (ahead).
Il precarico fisso può essere impostato in modo predeterminabile mediante uno spostamento di precarico definito (distanziale + forza di serraggio della ghiera), tenendo conto delle tolleranze di accoppiamento e dei differenziali di temperatura.
3. Parametri di impostazione
3.1 Carico minimo
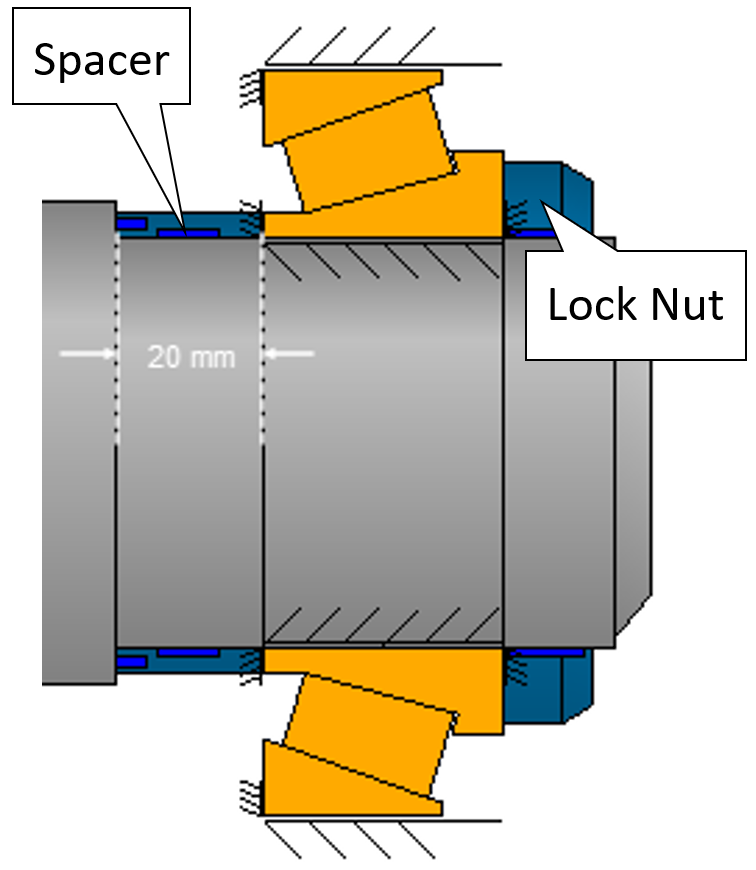
Figura 8
Lo spostamento di precarico viene selezionato, mediante variazione parametrica della lunghezza del distanziale con valore nominale di 20 mm (figura 8), in modo tale che la pressione minima sui rulli (pmin) rimanga, per quanto possibile, nettamente superiore a zero anche nell’elemento critico dello spettro di carico.
3.2 Durata di vita
Deve essere individuato un compromesso tra carico minimo e durata di vita, quest’ultima correlata alla potenza dissipata per attrito dovuta al precarico.
3.3 Forza di serraggio della ghiera sull’albero
La forza di serraggio della ghiera viene determinata come somma dei contributi di forza necessari al serraggio complessivo, quali la forza di spostamento dei cuscinetti (forza di montaggio), la forza di precarico del pacco cuscinetti e una forza di ritenuta aggiuntiva. Essa viene quindi impostata in modo da garantire il mantenimento del precarico obiettivo dell’insieme dei cuscinetti.
3.4 Zone di tolleranza
Infine, sulla base dei risultati di una variazione parametrica, viene analizzato il comportamento del sistema nelle combinazioni delle zone di tolleranza degli accoppiamenti e dei corrispondenti gradienti di temperatura, al fine di confermare l’impostazione selezionata.
4. Metodologia per la determinazione dei valori di riferimento
4.1 Espansione elastica degli anelli
Sotto precarico assiale, in presenza di accoppiamenti con gioco, l’anello esterno può espandersi radialmente sotto l’effetto dell’angolo di contatto, mentre l’anello interno può contrarsi. Entrambi i fenomeni riducono il precarico effettivo in esercizio. Tali effetti vengono considerati nel calcolo insieme alle condizioni di accoppiamento e ai differenziali di temperatura, affinché lo spostamento di precarico impostato raggiunga il valore obiettivo in esercizio. Per questo motivo, la considerazione della espansione elastica degli anelli è attivata per entrambi i cuscinetti.
4.2. Modello di calcolo esteso
Outboard, B1:
Il “modello di calcolo esteso” (figura 9) consente di definire elementi per i contatti assiali e radiali. Esso permette inoltre di considerare il gioco assiale tra l’anello del cuscinetto e l’albero oppure l’alloggiamento.
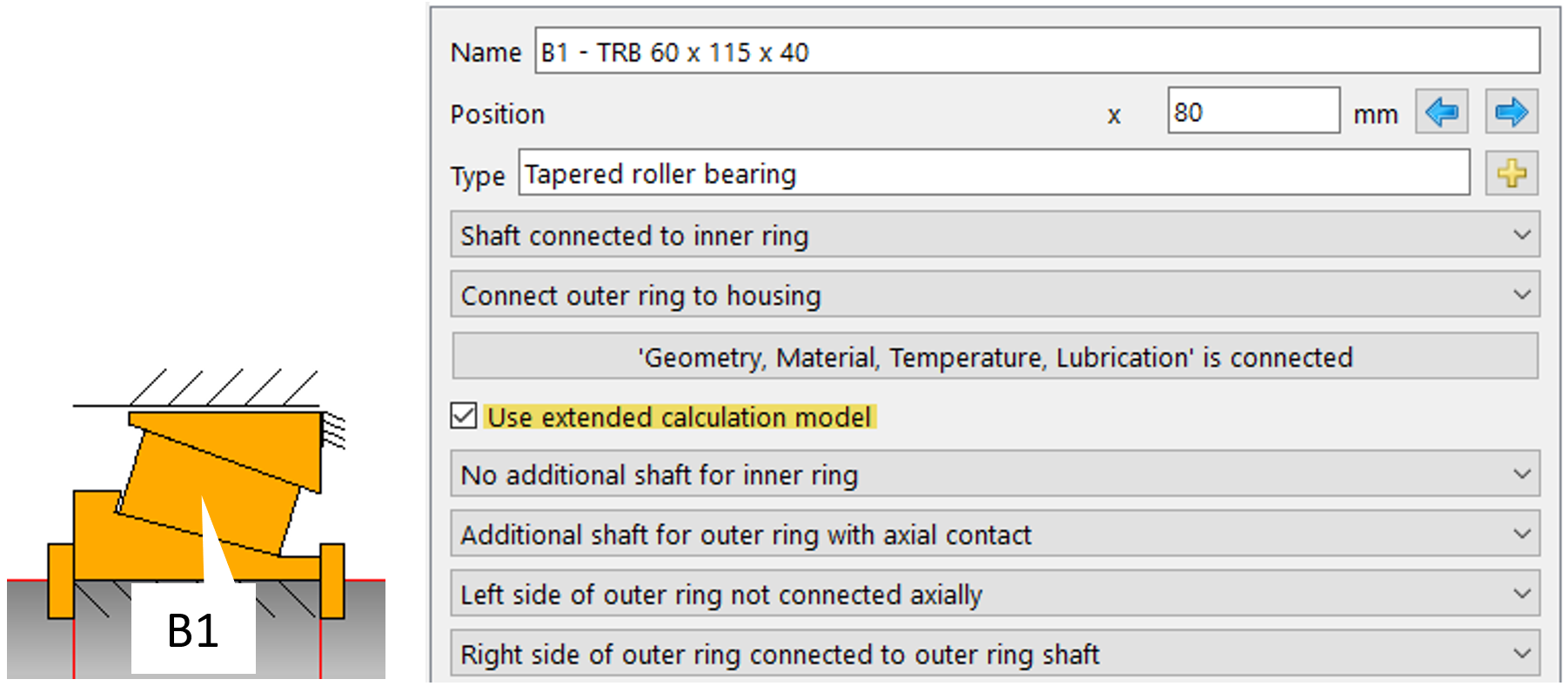
Figura 9
Inboard, B2:
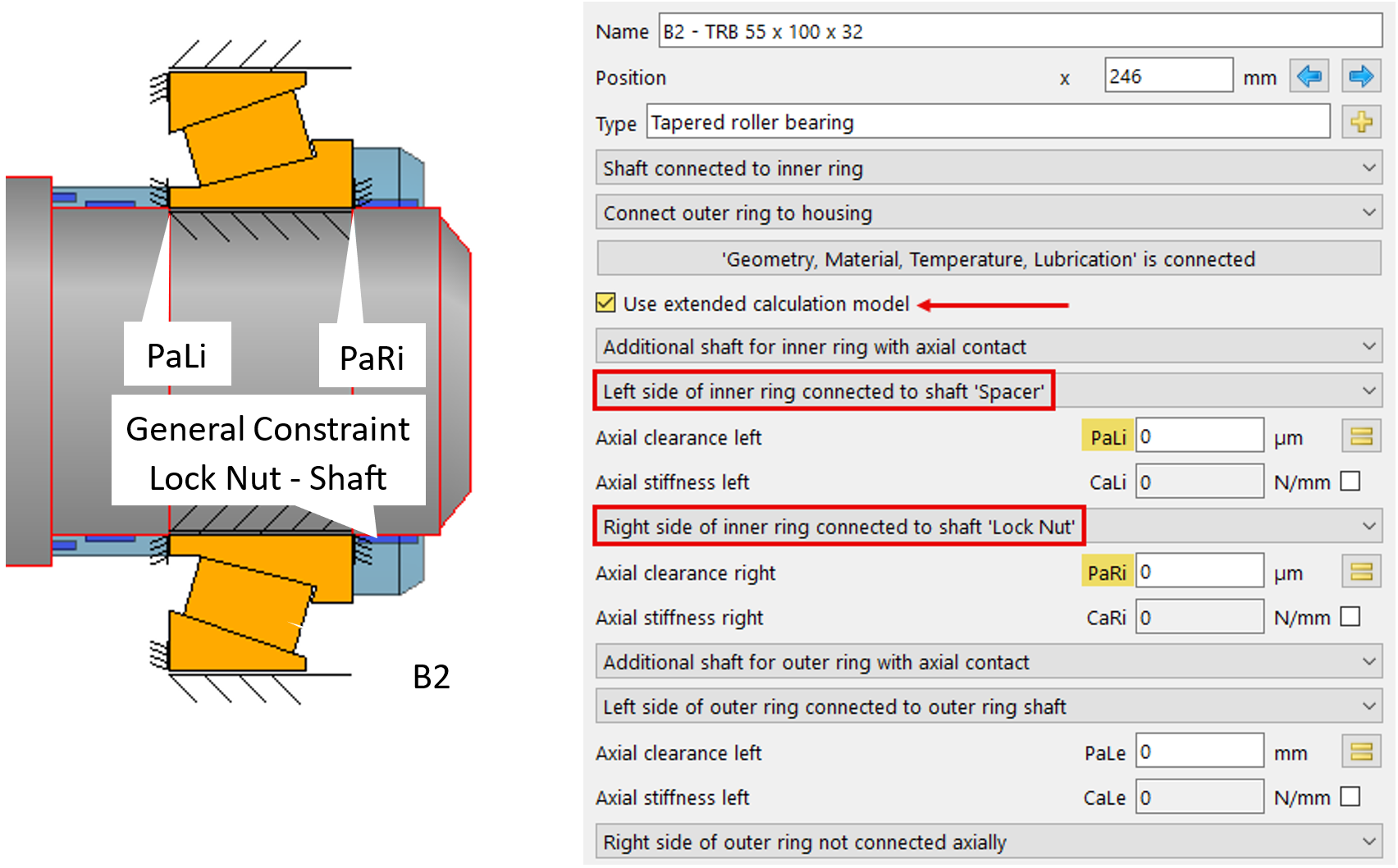
Figura 10
4.3 Spettro di carico
Viene attivato uno spettro di carico ipotetico secondo la tabella 1:
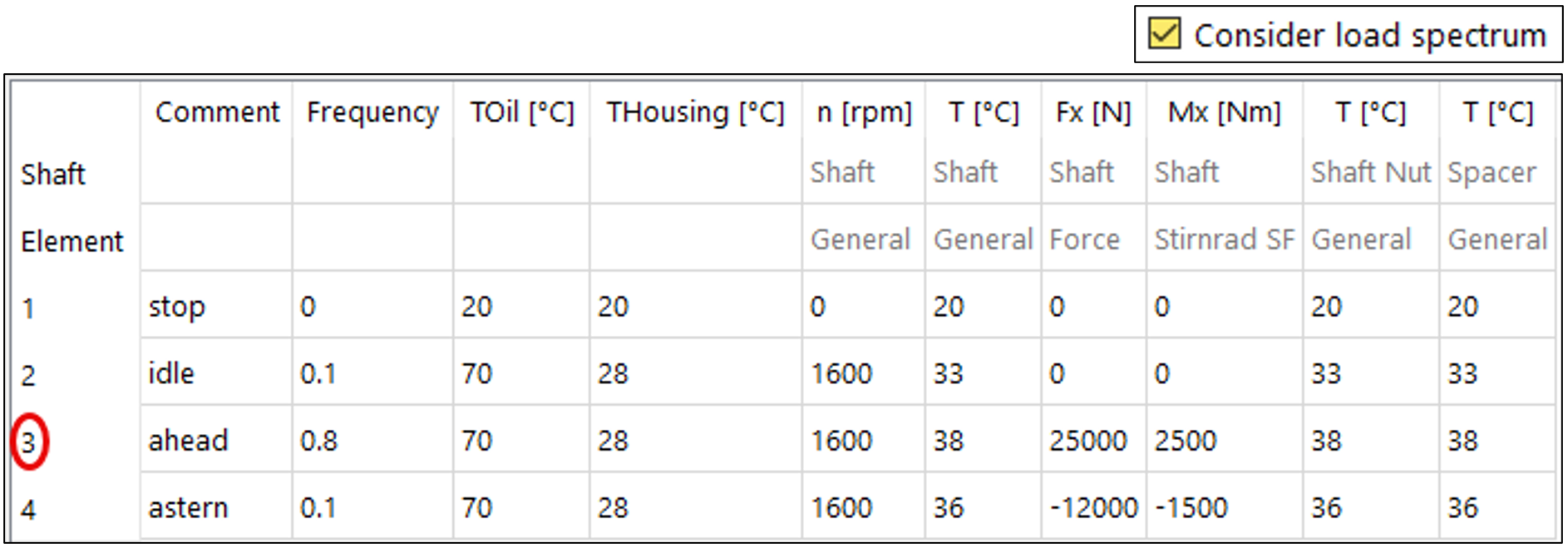
Tabella 1
L’elemento 3 è da considerarsi la condizione critica e pertanto di maggiore interesse in relazione al carico sui cuscinetti, al ribaltamento e allo slittamento (tabella 1).
4.4 Accoppiamenti
4.4.1 Generalità

Figura 11
La classe di precisione, gli accoppiamenti, le rugosità e i diametri dell’alloggiamento secondo la figura 11 sono presi in considerazione. Le impostazioni riportate nel report delle tolleranze generano, per B2 nello spettro di carico – elemento 1, le forze di montaggio descritte al punto 4.6.2.
4.4.2 Zone di tolleranza degli accoppiamenti
Un’analisi preliminare volta a determinare lo spostamento di precarico ideale viene opportunamente condotta assumendo una zona di tolleranza a gioco medio. In una fase successiva, al fine di una possibile verifica di robustezza rispetto a tutte le condizioni, dovrebbero tuttavia essere eseguite anche analisi discostate dal valore medio.
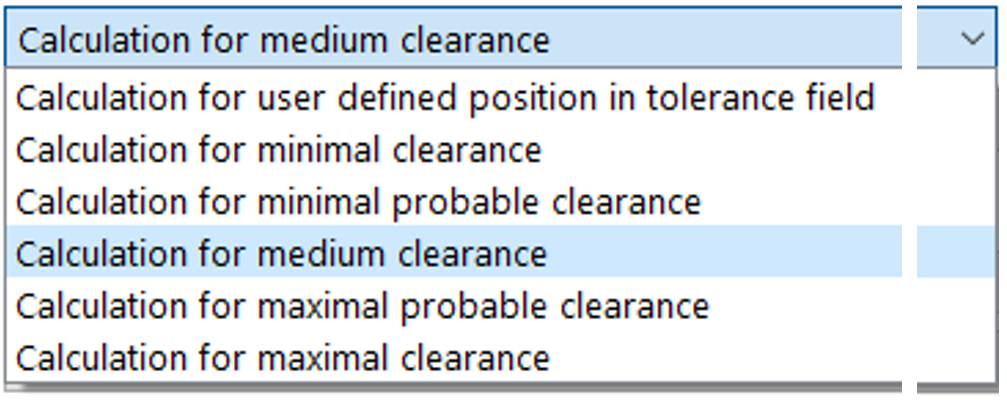
Figura 12
Un estratto del report delle tolleranze (tabella 2) mostra, per la condizione di montaggio a freddo (spettro di carico – elemento 1), le seguenti interferenze di accoppiamento in B1 e B2:

Tabella 2
4.5 Parametrizzazione dello spostamento di precarico
4.5.1 Parametri
La parametrizzazione dello spostamento di precarico viene eseguita con riferimento alla verifica del carico minimo nell’elemento critico 3 dello spettro di carico.
l parametro B2-Pa_Li è idoneo a rappresentare la variazione dello spostamento di precarico attraverso la sua definizione di gioco assiale tra il distanziale e l’anello interno B2 (figura 10). In 20 passi, la riduzione assiale del distanziale deve rappresentare, tramite Pa_Li, la generazione di gioco assiale tra il distanziale e l’anello interno del cuscinetto B2. La concomitante interferenza negativa tra l’anello interno e la ghiera sull’albero Pa_Ri (figura 10) deve allo stesso tempo rappresentare uno spostamento verso sinistra dell’anello interno pari ai valori parametrizzati.
4.5.2 Valutazione sotto posizionamento medio delle tolleranze
Si può assumere che un aumento del precarico comporti anche un incremento della temperatura dell’albero, del distanziale e della ghiera sull’albero (figura 13):
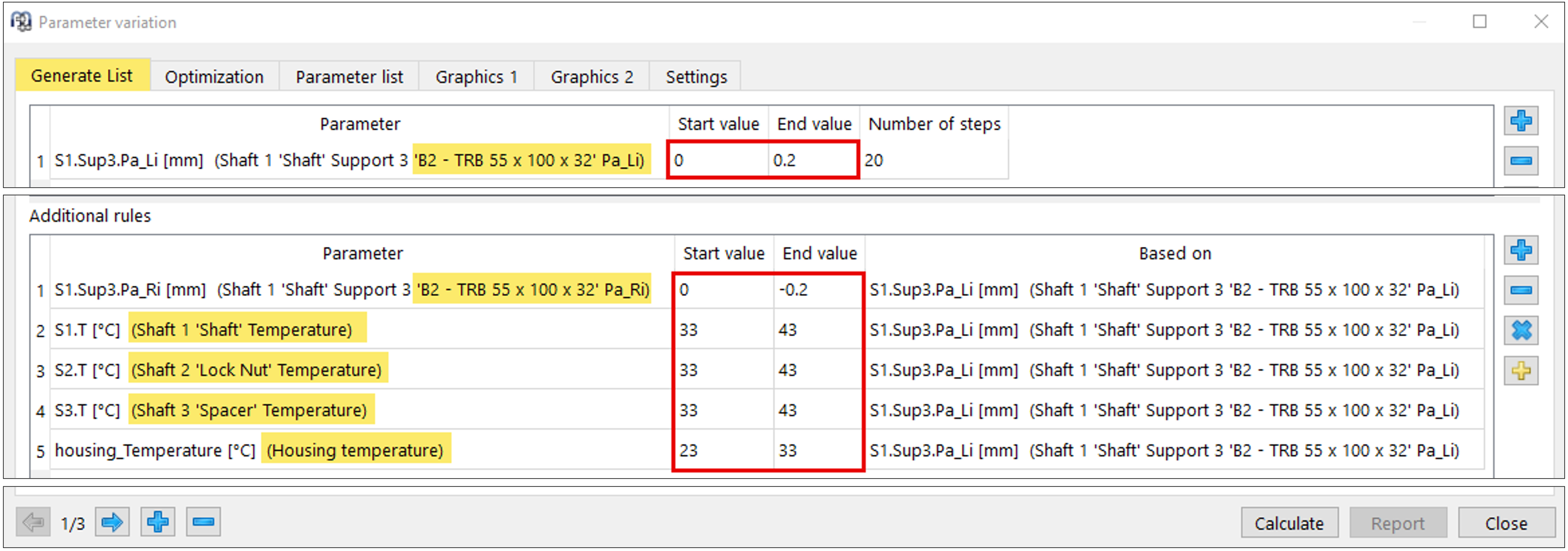
Figura 13
Nella pratica, le temperature qui assunte hanno spesso un carattere puramente ipotetico o empirico, poiché misurazioni corrispondenti risultano nella maggior parte dei casi tecnicamente o economicamente impegnative.
La parametrizzazione in condizioni di interferenza di accoppiamento corrispondenti al “valore medio”, ossia il “calcolo per gioco medio” su entrambi i cuscinetti (figura 12), fornisce, per le tensioni di contatto e per la vita di riferimento modificata nello spettro di carico – elemento 3, le seguenti curve (figura 14):
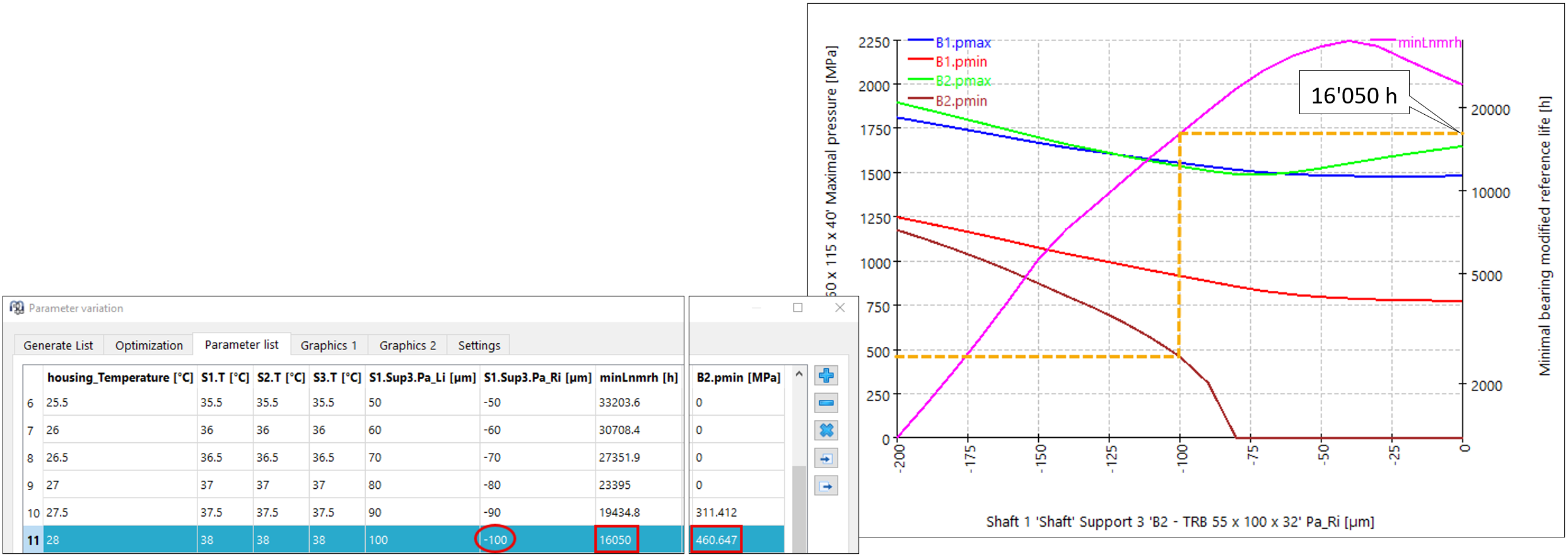
Figura 14
Uno spostamento di precarico di 100 µm appare, per la condizione critica di B2.pmin, con circa 460 MPa, pmin > 0 e una durata di vita corrispondente superiore al valore richiesto, come una condizione praticabile, come si evince dall’elenco parametri riportato sopra.
Con la vita di riferimento modificata risultante sarebbero soddisfatti i primi due requisiti della definizione degli obiettivi. La considerazione sopra riportata può costituire, per un singolo caso, il procedimento corretto qualora siano note le specifiche zone di tolleranza degli accoppiamenti e sia disponibile un’approssimazione del gradiente di temperatura. Per una produzione in serie è necessario un ulteriore supporto di calcolo, al fine di poter valutare rapidamente anche combinazioni casuali di interferenze di accoppiamento interne ed esterne. Il paragrafo seguente intende mostrare un possibile approccio mediante l’utilizzo di uno studio parametrico specifico in MESYS.
4.5.3. Analisi in funzione delle zone di tolleranza
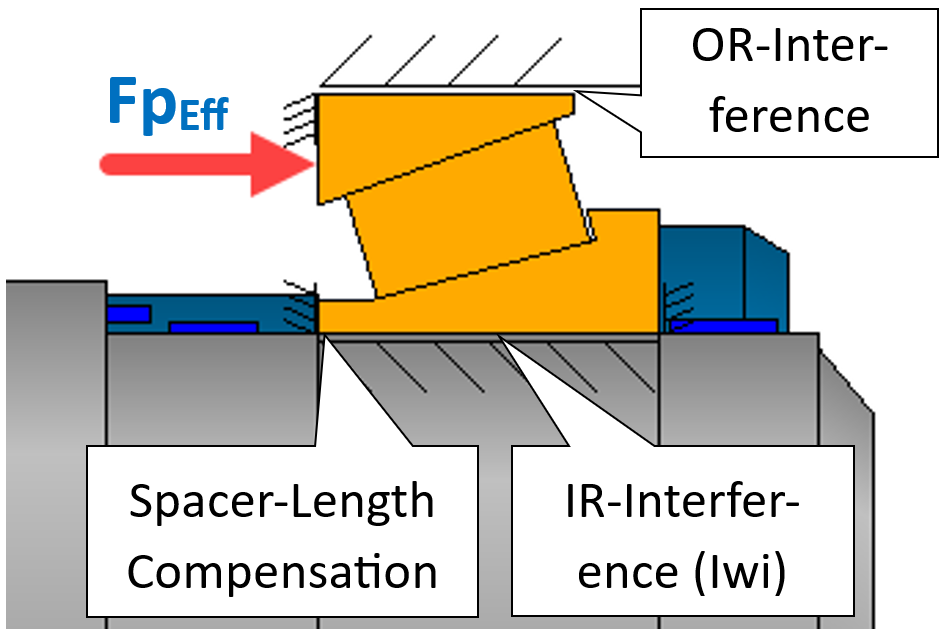
Figura 15
La forza di precarico effettiva del cuscinetto (FpEff) rappresenta il contributo dominante della forza totale di serraggio da applicare alla coppia di cuscinetti. Se è possibile determinare, per ogni combinazione delle interferenze di accoppiamento di entrambi i cuscinetti, una lunghezza del distanziale adeguata e compensativa, si può assumere che la forza di precarico effettiva (FpEff) rimanga costante. Un tale approccio può essere individuato mediante una funzione di ottimizzazione nell’ambito della variazione parametrica e costituisce pertanto un ausilio interessante per una produzione in serie.

Figura 16
Caso di riferimento:
Un caso di riferimento (figura 16), con una lunghezza del distanziale corrispondente posizionata al centro delle possibili zone di tolleranza per entrambi i cuscinetti, deve fornire un riferimento per il rispettivo adeguamento necessario della lunghezza del distanziale.
Generazione delle variabili:
Una suddivisione pratica dei valori iniziali e finali delle interferenze di accoppiamento è finalizzata a migliorare la chiarezza dei risultati (figura 17).

Figura 17
Ottimizzazione:
MESYS consente, nell’ambito della variazione parametrica, anche l’opzione di ottimizzazione “minimizzare un input in base a vincoli”. In questo modo è possibile minimizzare una variabile soggetta a regole e condizioni aggiuntive. La funzione è idonea a minimizzare la variazione della lunghezza del distanziale (Δ spacer), espressa tramite i parametri PaLi e PaRi (figura 18).
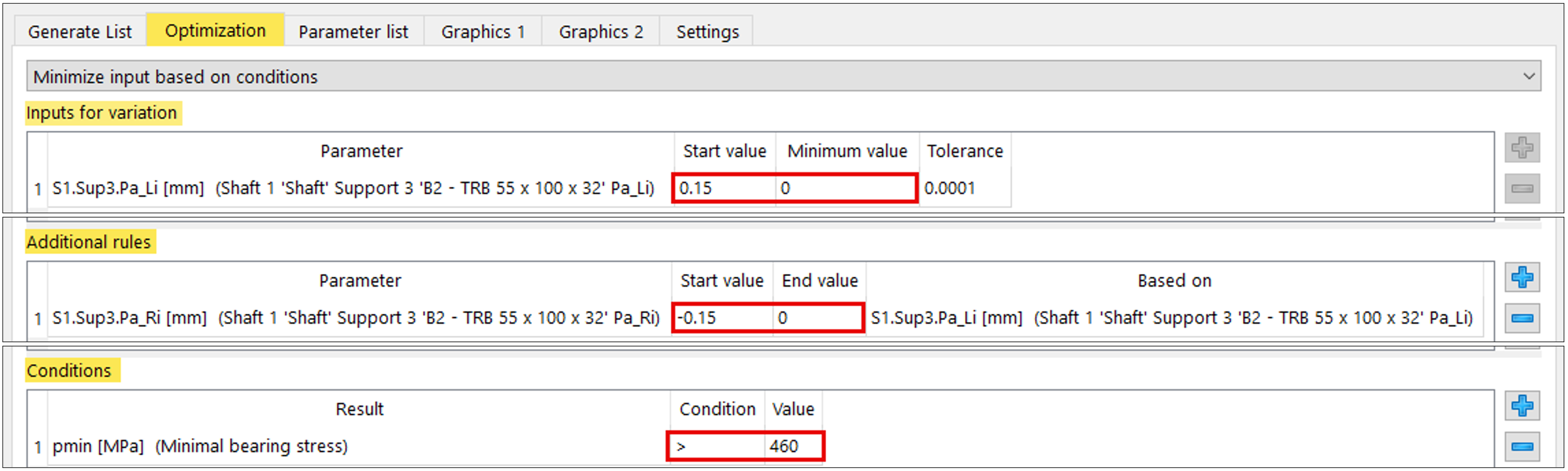
Figura 18
La parametrizzazione deve essere eseguita separatamente per ciascun cuscinetto, B1 e B2, includendo lo spettro di carico.
Esportazione:
Mediante il comando di esportazione (figura 19), gli elenchi dei parametri di B1 e B2 possono ora essere ulteriormente elaborati in Excel (figura 20).
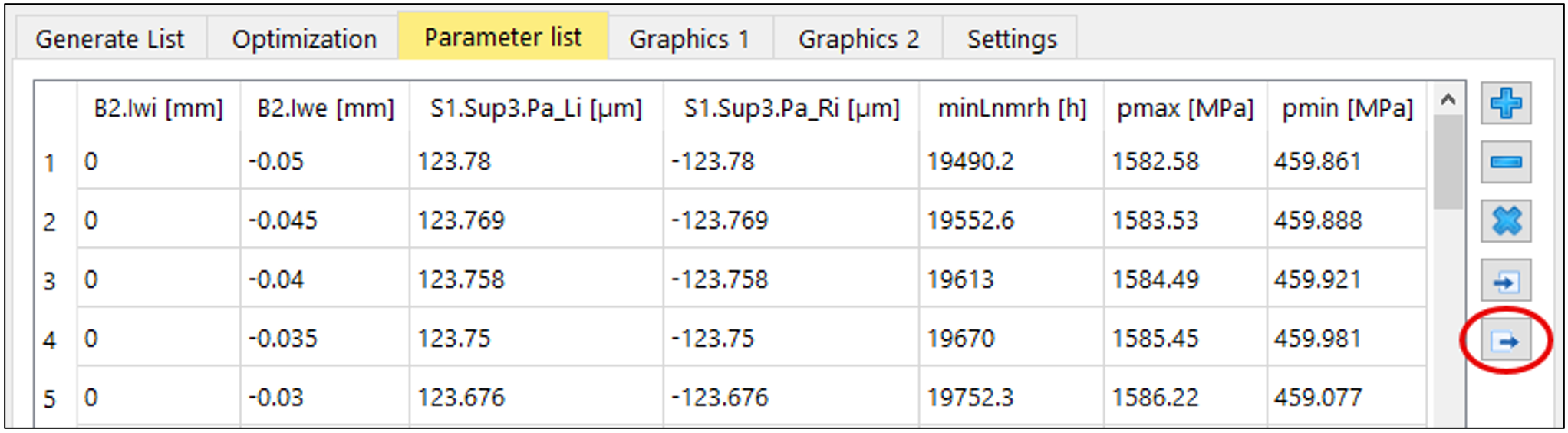
Figura 19
The incremental representation can be transposed into a matrix (Figure 20) and, in a subsequent step, converted into rounded approximate values for practical use:
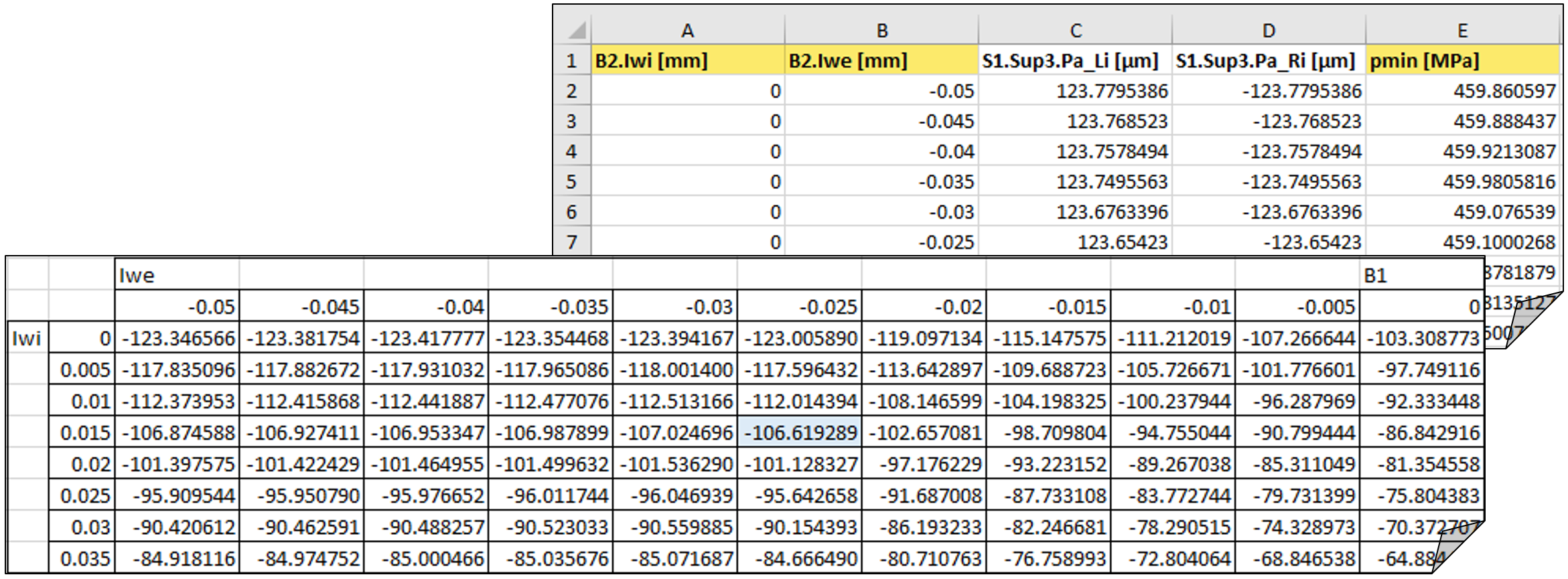
Figura 20
Ciò consente di creare una matrice pratica per entrambi i cuscinetti a rulli conici, che fornisce le deviazioni dalla dimensione nominale del distanziale in funzione delle dimensioni effettive del segmento d’albero e del cuscinetto (tabella 3):
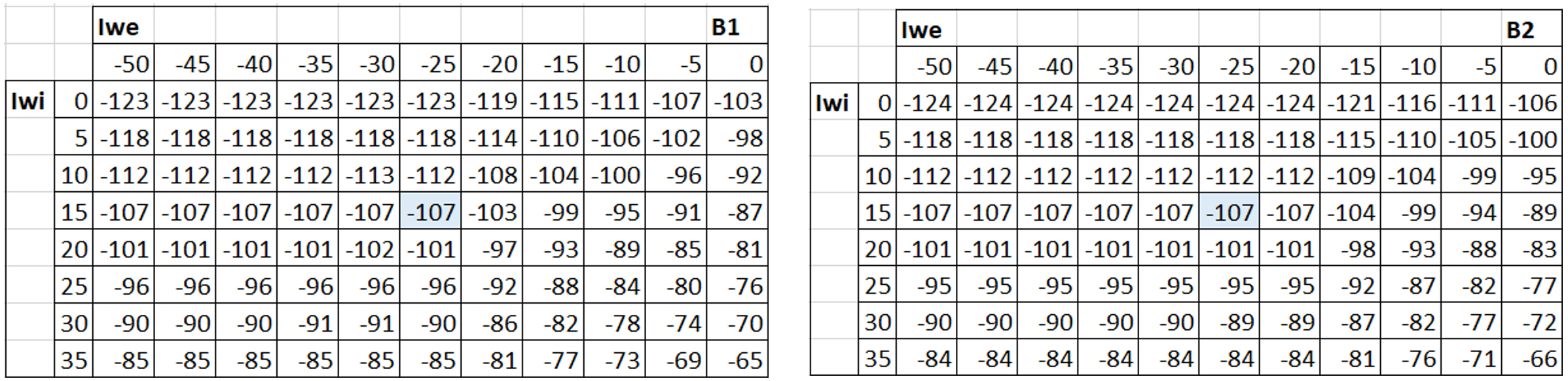
Tabella 3
4.5.4 Calcolo del distanziale
La lunghezza del distanziale può ora essere determinata in modo approssimato sulla base delle rispettive deviazioni rispetto al caso di riferimento, come illustrato nel seguito.
Determinazione della lunghezza del distanziale mediante iterazione nel caso di riferimento
La deviazione della lunghezza del distanziale rispetto al valore nominale può essere determinata, in presenza delle interferenze di riferimento (figura 16) e con lo spettro di carico attivato, mediante l’applicazione di una iterazione puntuale eseguita manualmente, fino al raggiungimento di pmin = 460 MPa (figura 21).

Figura 21
Tale grandezza viene di seguito indicata come ‘deviazione della lunghezza del distanziale rispetto alla lunghezza nominale nel caso di riferimento’, PaRiRef.
Lunghezza del distanziale tramite valore medio nel caso di riferimento
PaRiRef può inoltre essere approssimato mediante il valore medio dei due valori PaRi calcolati per B1 e B2 (tabella 3), che, arrotondato secondo questo approccio, fornisce anch’esso −107 µm.
Lunghezza del distanziale per deviazione rispetto al caso di riferimento
A partire dalla tabella 3 può essere costruita una matrice maggiormente orientata alla produzione, che riporti esclusivamente la deviazione rispetto a PaRiRef. Se quest’ultima viene indicata come delta_PaRiRef e PaRi rappresenta la posizione di tolleranza PaRiTol, il valore di riferimento PaRiRef nella matrice viene compensato di −107 (tabella 4). Nel caso in cui PaRiTol ≙ PaRiRef per il campo di tolleranza considerato, risulta delta_PaRiRef = 0:
ΔPaRiRef = PaRiTol – PaRiRef
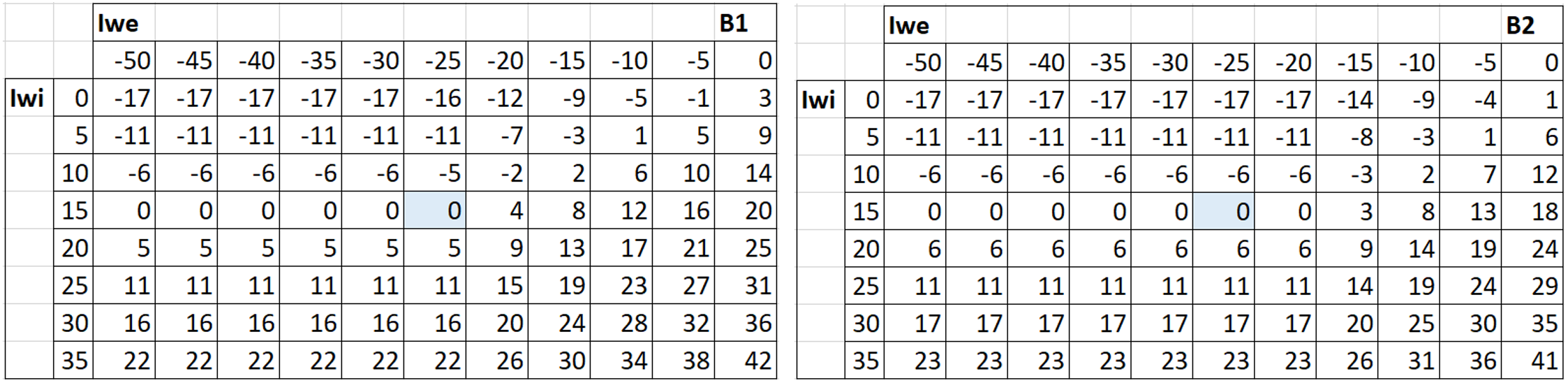
Tabella 4
Determinazione della lunghezza nominale del distanziale
Siano indicate la lunghezza di riferimento del distanziale con RSL, la lunghezza obiettivo del distanziale con TSL e la lunghezza nominale del distanziale con NSL; valgono pertanto le seguenti relazioni:
RSL = NSL + PaRiRef = 20 + (-0.107) = 19.893 mm
TSL = RSL + B1.ΔPaRiRef + B2.ΔPaRiRef
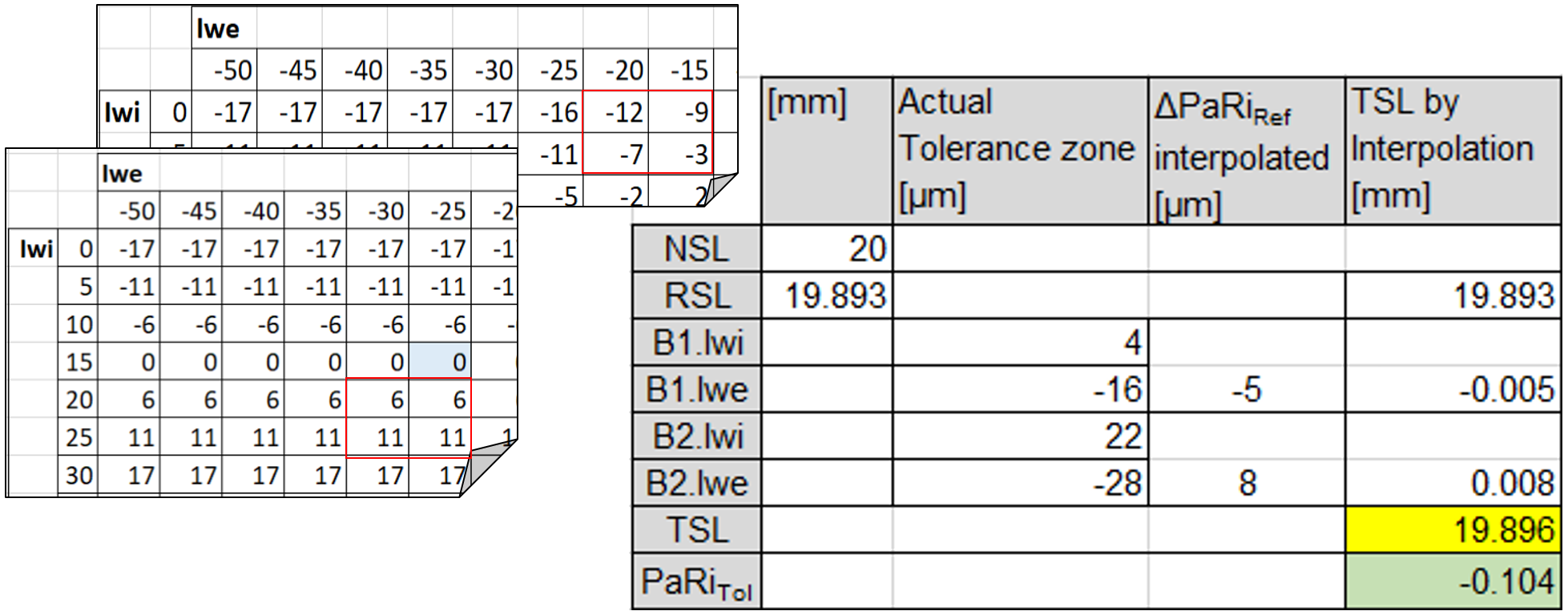
Tabella 5
L’esempio a destra mostra la determinazione pratica della riduzione del distanziale mediante l’utilizzo della matrice semplificata di cui alla tabella 4 e l’applicazione dell’interpolazione bilineare (tabella 5):
L’esecuzione del calcolo, con l’inserimento delle zone di tolleranza e della riduzione del distanziale dell’esempio precedente, mostra che la condizione di carico minimo con valore obiettivo di 460 MPa viene rispettata (figura 22).

Figura 22
4.6 Forza di serraggio della ghiera di bloccaggio
4.6.1 Generalità
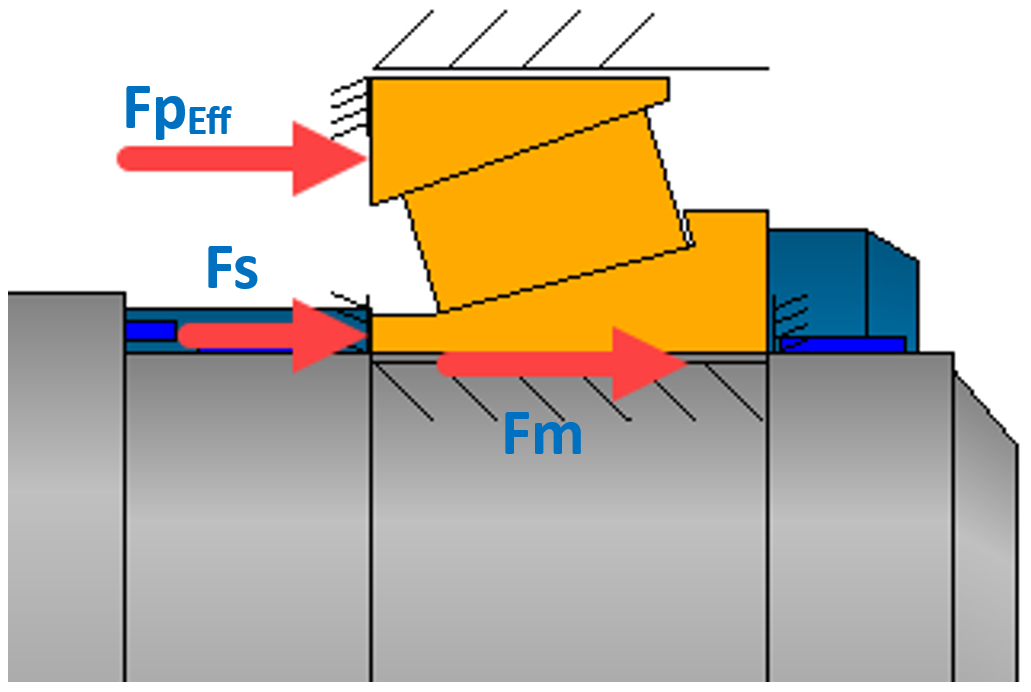
Figura 23
La determinazione della forza di serraggio necessaria della ghiera sull’albero dovrebbe essere effettuata, in modo appropriato, nella condizione di montaggio, ossia per l’elemento 1 dello spettro di carico. La forza di serraggio della ghiera viene generalmente ricavata nel corso della determinazione analitica della coppia di serraggio della ghiera stessa. L’approccio di approssimazione adottato combina la forza di montaggio (a freddo), la forza di precarico della coppia di cuscinetti e una forza di ritenuta aggiuntiva nella forza totale di serraggio richiesta (figura 23).
- Forza di montaggio Fm
- Forza di precarico della coppia di cuscinetti FpEff
- Forza di ritenuta aggiuntiva Fs
4.6.2. Forza di montaggio
La forza di montaggio (Fm) deve essere quantificata, a fronte di una procedura di montaggio corretta, esclusivamente sul lato interno (Ffit_i; tabella 6). Qualora i cuscinetti vengano montati senza differenziale di temperatura, la forza di montaggio può essere trascurata.
Coefficiente di attrito
Se nelle opzioni del cuscinetto è definito un coefficiente di attrito per il montaggio (figura 24), nel report delle tolleranze viene visualizzata anche una forza di montaggio assiale.
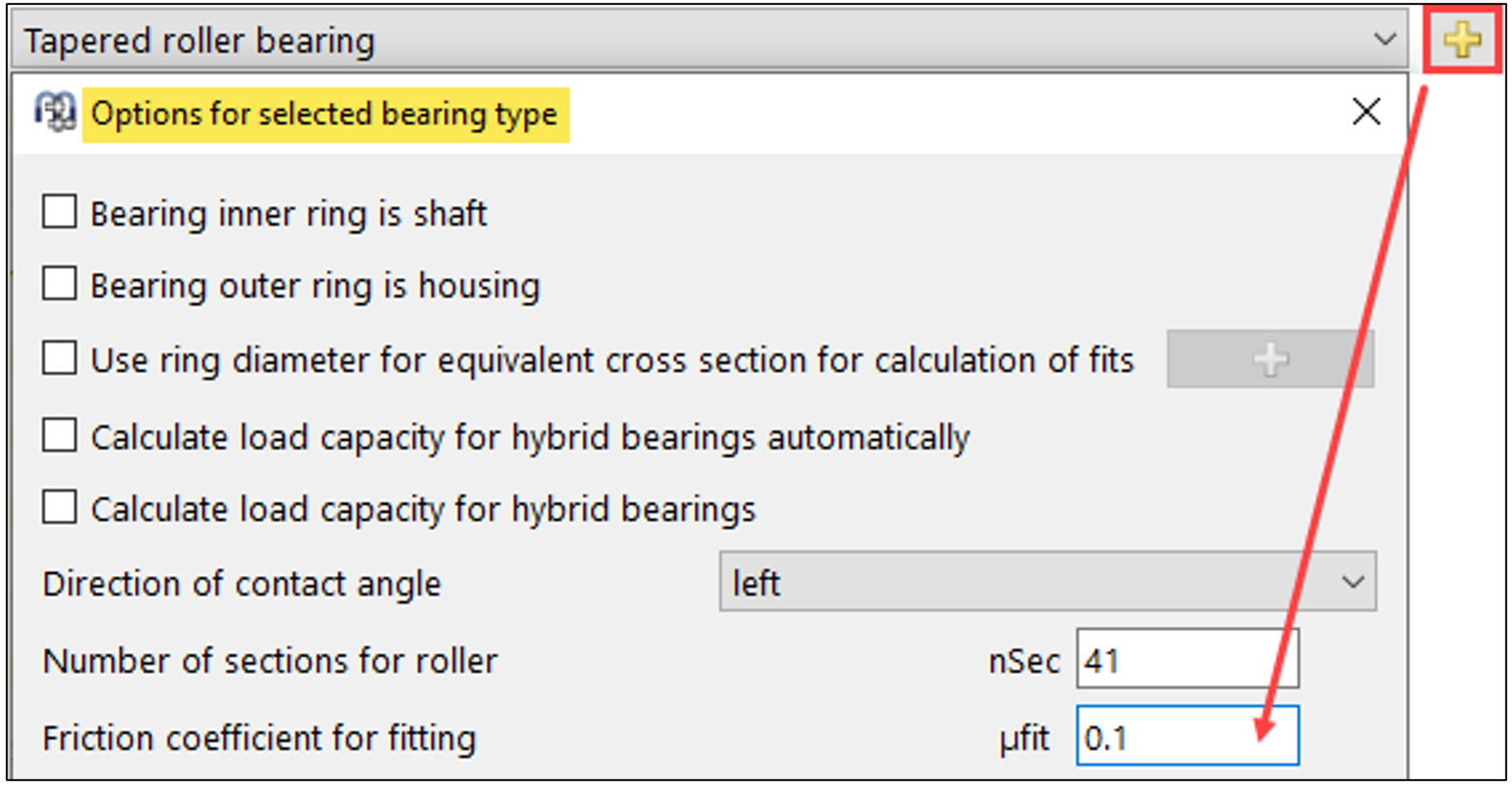
Figura 24
Forza di montaggio specifica
Tramite il report delle tolleranze relativo al cuscinetto B2, la forza di montaggio può essere visualizzata direttamente (tabella 6).
La forza di montaggio (Fm) è qui leggibile come intervallo minimo–massimo e, tenendo conto dell’espansione elastica degli anelli, si riferisce alle tolleranze di accoppiamento selezionate. I valori riportati in tabella 6 corrispondono al cuscinetto B2 nell’elemento 1 dello spettro di carico, nel caso di riferimento iterato (figura 21).

Tabella 6
Forza di montaggio in funzione delle zone di tolleranza
Le informazioni sulla forza di montaggio fornite dal report delle tolleranze non sono sufficienti come base per una produzione industriale. A tale scopo, MESYS offre la possibilità di determinare le forze di montaggio considerando combinazioni delle zone di tolleranza mediante variazione parametrica.
Il file di esportazione della lista parametri derivante dal calcolo della riduzione del distanziale per il cuscinetto B2 (figura 19) consente ora di determinare la forza di montaggio per tutte le combinazioni possibili delle zone di tolleranza degli accoppiamenti nell’intervallo considerato.
L’effetto risultante della forza assiale della coppia di cuscinetti precaricata può essere considerato come un valore compensato, riconducibile all’adattamento del distanziale.
Parametri quali la forza di montaggio B2.Ffit o la forza assiale sulla ghiera dell’albero S2.Sup1.Fx possono essere, in questa fase, aggiunti ulteriormente all’elenco dei parametri (figura 25).
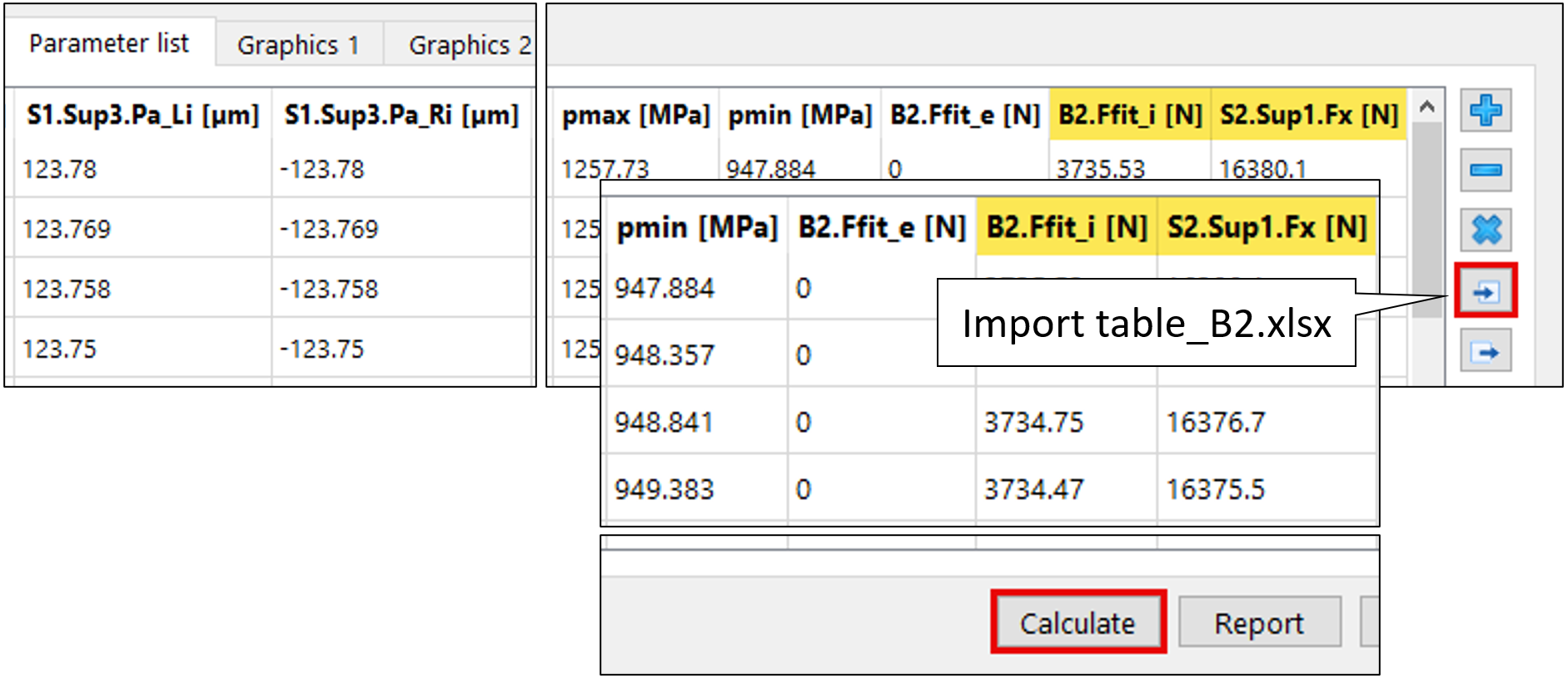
Figura 25
Il file importato con riferimento all’elemento 1 dello spettro di carico (montaggio) genera ora, dopo l’attivazione del passo di calcolo, oltre alle forze di montaggio interne ed esterne per B2 (Ffit), anche la forza di serraggio della coppia di cuscinetti sulla ghiera dell’albero S2.Sup1.Fx (figura 25).
In tal modo viene rappresentata, con un’approssimazione adeguata, la dipendenza della forza di montaggio sul cuscinetto B2 dalle interferenze di accoppiamento e dagli effetti dell’espansione elastica degli anelli.
4.6.3 Forza di ritenuta aggiuntiva
Una forza di ritenuta aggiuntiva (Fs) per il blocco precaricato viene applicata nella pratica in via preventiva, al fine di fornire una rigidezza supplementare per la compensazione di azioni di carico dinamiche.
A tal fine, per il valore di tensione di contatto (MPa) all’interferenza con il distanziale, può essere adottato un valore basato su indicazioni dei produttori di cuscinetti oppure derivato tramite un approccio empirico.
La forza Fs, come termine additivo alla forza di serraggio della ghiera, viene qui assunta pari a 8 000 N.
4.6.4 Forza di serraggio totale
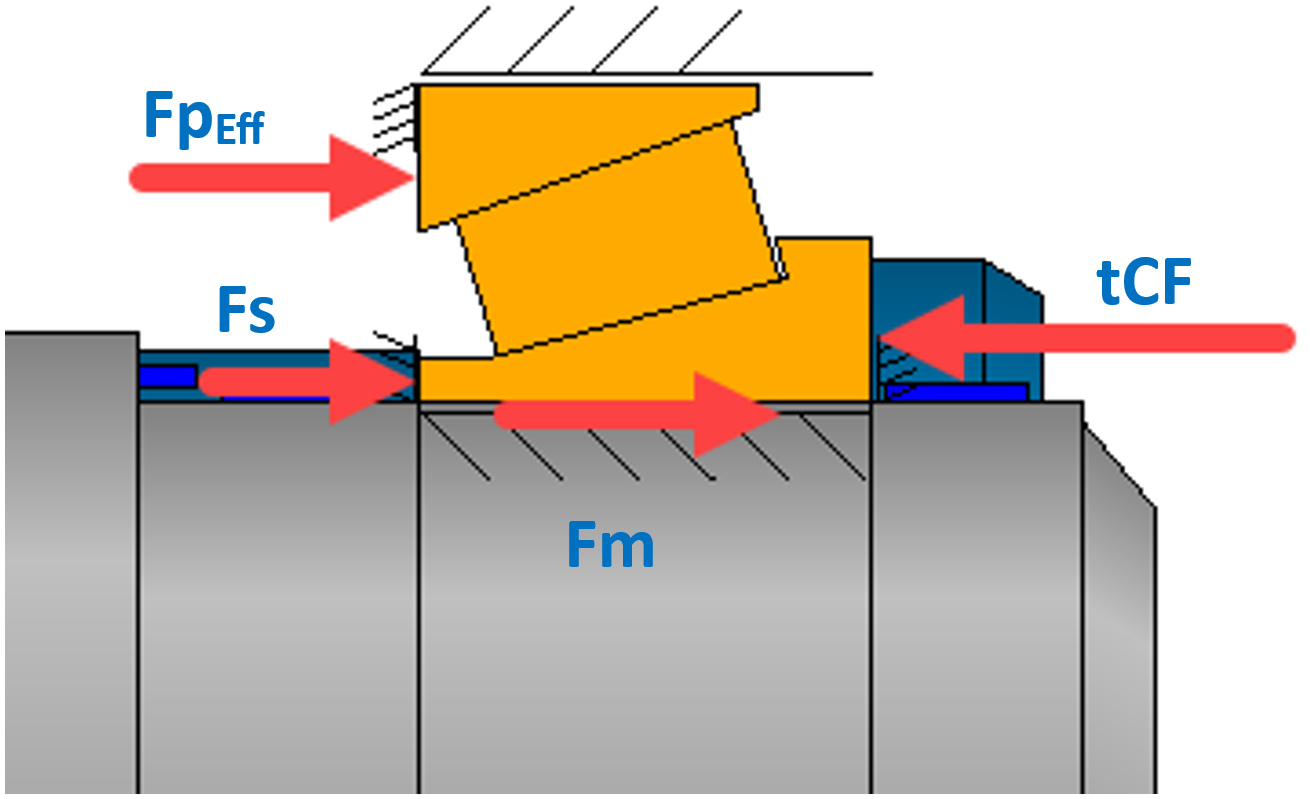
Figura 26
La forza di serraggio totale prevista della ghiera (tCF) (figura 26), risultante dalla somma della forza di precarico effettiva della coppia di cuscinetti + forza di montaggio + forza di ritenuta aggiuntiva, si esprime secondo la definizione precedente come segue:
tCF = Fm+ FpEff + Fs
Mediante l’aggiunta di un valore costante per Fs secondo il punto 4.6.3 in un file di esportazione (figura 27), si ottiene ora uno strumento pratico per la determinazione rapida della forza di serraggio della ghiera sull’albero associata a una specifica lunghezza del distanziale.
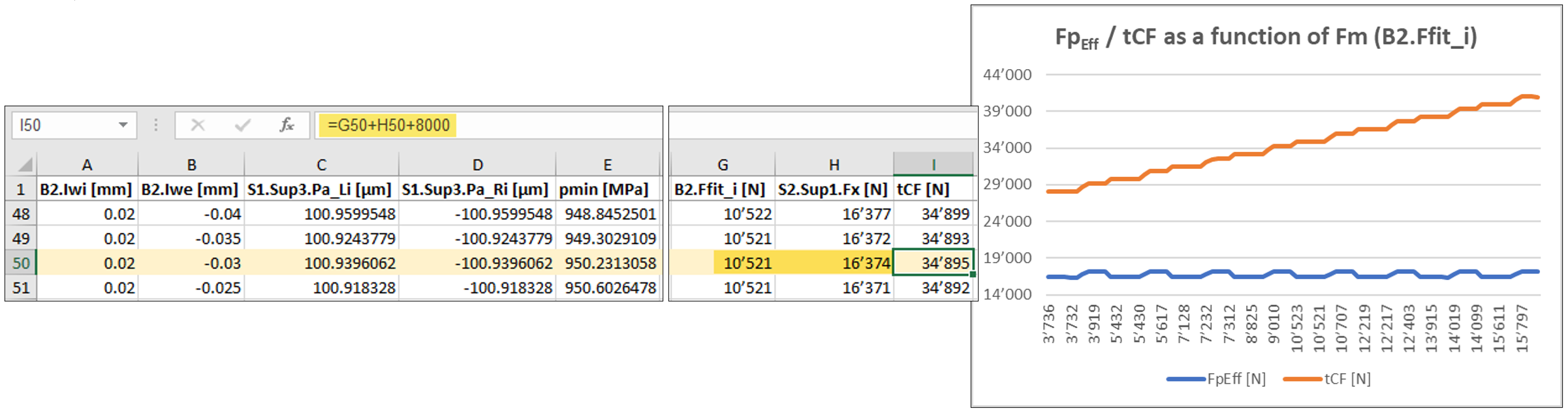
Figura 27
Il grafico di figura 27 mostra che, sotto l’effetto dell’adeguamento del distanziale, la forza di precarico del cuscinetto FpEff (S2.Sup.Fx) rimane quasi costante al variare della forza di montaggio interna (B2.Ffit_i).
Questo effetto non si modifica neppure in caso di scostamento dalla zona di tolleranza di riferimento del cuscinetto B1. L’approccio descritto al punto 4.5.4 tiene infatti conto di un adeguamento del distanziale sotto l’influenza di entrambe le sedi dei cuscinetti. In tal senso, come approssimazione qualitativa, la derivazione della forza di serraggio necessaria della ghiera sull’albero in funzione della variazione della zona di tolleranza del cuscinetto da precaricare B2, unitamente all’arrotondamento o all’interpolazione dell’elenco dei parametri importato al punto 4.6.2, può essere considerata un approccio appropriato.
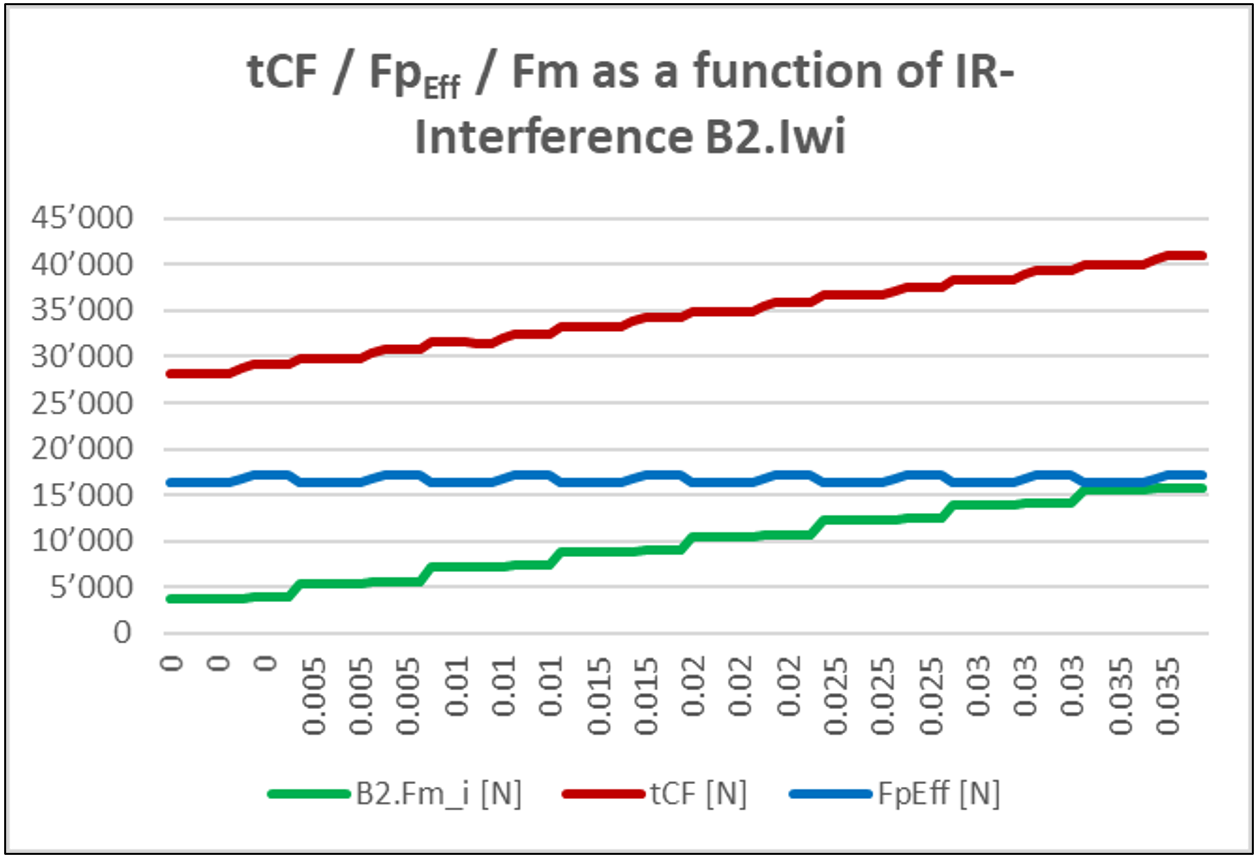
Figura 28
I termini additivi della forza di serraggio della ghiera sull’albero Fm + FpEff + Fs possono essere arrotondati o interpolati singolarmente. Grazie all’adeguamento del distanziale su tutte le zone di tolleranza – inclusa l’interferenza esterna – la forza di precarico del cuscinetto FpEff rimane quasi costante (figura 28). La variazione della forza totale di serraggio necessaria della ghiera tCF è pertanto da ricercarsi nella forza di montaggio sull’anello interno. Ne consegue che la zona di tolleranza esterna e la relativa interferenza (Iwe) non risultano qui rilevanti e che, ai fini pratici, una considerazione monodimensionale è pienamente adeguata.
Per la specifica condizione di tolleranza, la forza di montaggio Fm risulta pari a 10 521 N e la forza di precarico del cuscinetto FpEff pari a 16 374 N. Da ciò deriva una forza di serraggio della ghiera sull’albero tCF pari a 34 895 N (figura 27).
5. Effetto e verifica
5.1 Esempio
Sulla base del calcolo di esempio della lunghezza del distanziale al punto 4.5.4, deve essere determinata la forza di serraggio della ghiera sull’albero. La riduzione del distanziale (“rientro”, tabella 5) è stata determinata pari a −104 µm per una lunghezza obiettivo del distanziale SSL di 19,896 mm.
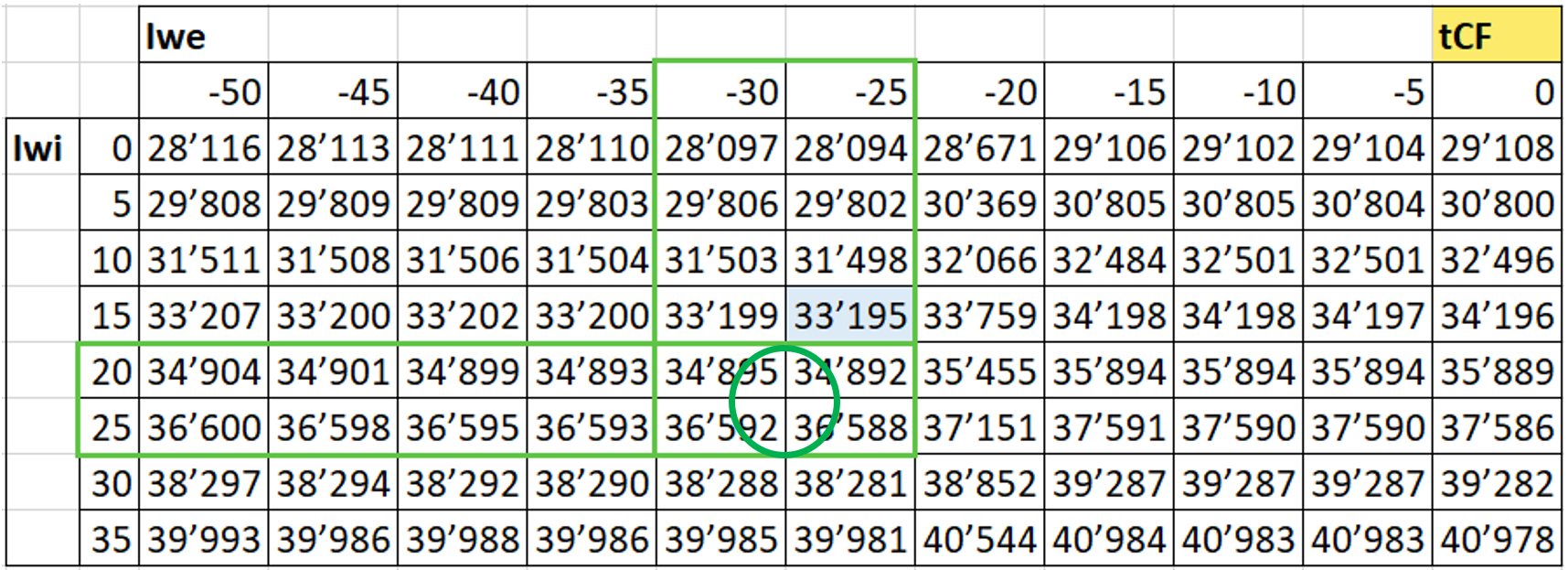
Tabella 7
Interpolazione bilineare di tCF
La tabella convertita in una rappresentazione matriciale e generata al punto 4.6.4 costituisce la base per la determinazione della forza di serraggio della ghiera sull’albero tCF (tabella 7).
Il valore della forza totale di serraggio della ghiera tCF, ottenuto mediante la corrispondente interpolazione, risulta pari a 35’572 N.
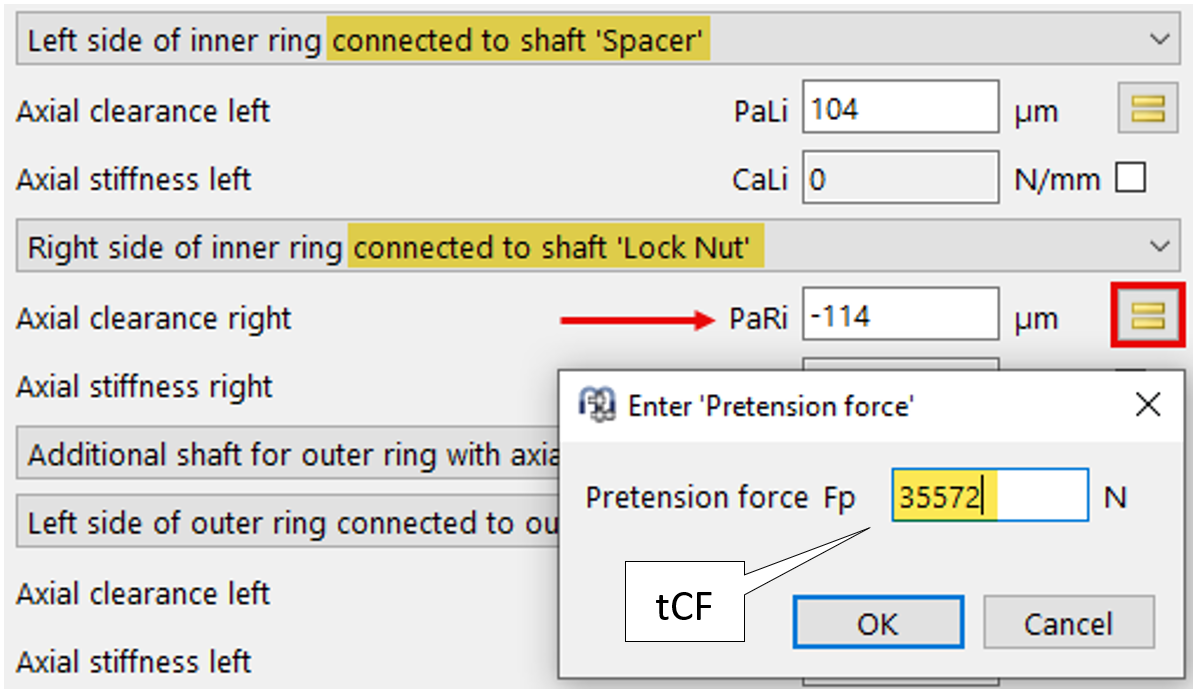
Figura 29
Poiché la forza di serraggio della ghiera sull’albero è ora nota, essa può essere impostata in MESYS in modo agevole tramite il pulsante “=” del parametro PaRi (figura 29).
Nota: la forza di serraggio della ghiera sull’albero può essere imposta anche come condizione al contorno direttamente sulla ghiera stessa.
5.2 Resultati
L’output dei risultati, a seguito dell’inserimento dei valori corrispondenti all’esempio precedente, mostra nella finestra inferiore dell’interfaccia utente le forze assiali, le tensioni di contatto e la durata di vita attese (figura 30).
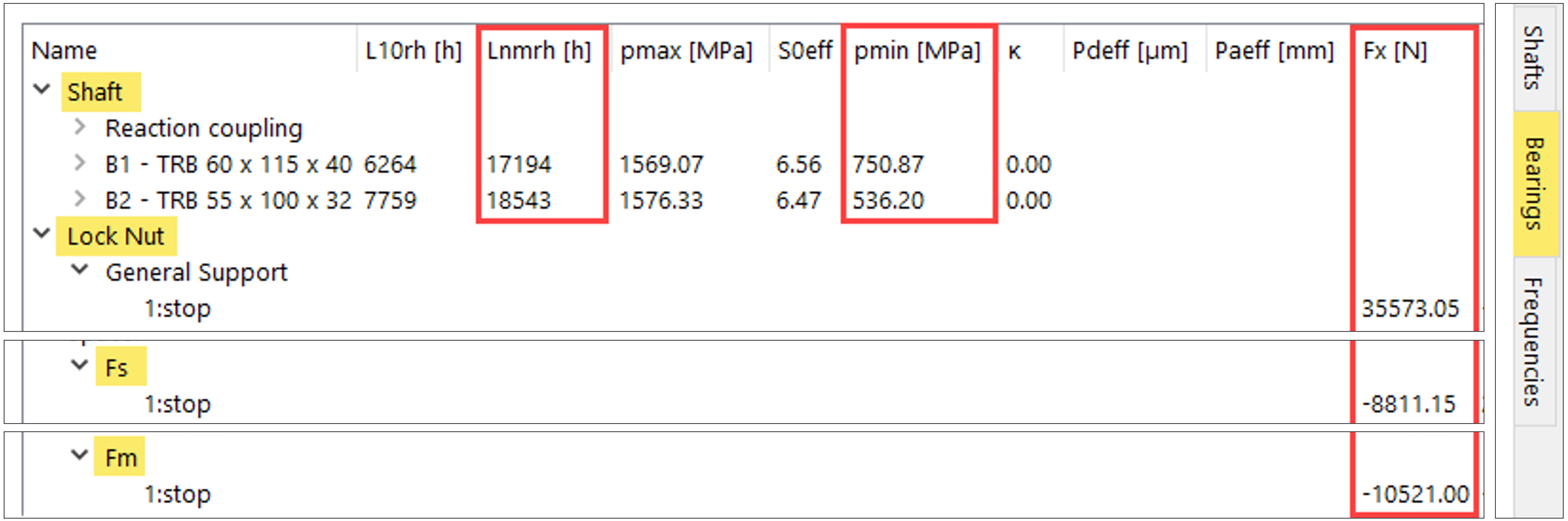
Figura 30
5.3 Verifica
Con riferimento agli obiettivi definiti e considerando l’intero spettro di carico, è possibile affermare quanto segue:
- Il carico minimo è rispettato
- La durata di vita minima è rispettata
- La forza di serraggio della ghiera sull’albero è progettata in modo specifico
- I metodi di approssimazione illustrati risultano robusti sull’intero intervallo delle zone di tolleranza degli accoppiamenti
5.4 Ulteriori osservazioni
La progettazione del precarico e della regolazione di una coppia di cuscinetti a rulli conici descritta nel presente documento non pretende di essere esaustiva. L’impostazione si basa su ipotesi che devono essere adattate al singolo caso applicativo. La rigidezza dei cuscinetti dipende dalla loro geometria interna, che spesso non è nota agli utilizzatori finali.


