Il software MESYS Calcolo Cuscinetti Volventi fornisce matrici di rigidezza tangente e matrici di cedevolezza (compliance) per i cuscinetti. Di seguito è riportato un esempio di matrice di rigidezza tangente per un cuscinetto radiale a sfere 6204-C3, soggetto a un carico radiale di 2 kN:
| ux [µm] | uy [µm] | uz [µm] | ry [mrad] | rz [mrad] | |
| Fx [N] | 6,870908 | 0 | 0 | 0 | -97,8685 |
| Fy [N] | 0 | 124,8287 | 0 | 0 | 0 |
| Fz [N] | 0 | 0 | 54,25732 | 0 | 0 |
| My [Nm] | 0 | 0 | 0 | 0,466423 | 0 |
| Mz [Nm] | -0,09968 | 0 | 0 | 0 | 1,461134 |
La rigidezza tangente indica di quanto varia il carico in seguito a una piccola variazione dello spostamento relativo a partire dal punto di lavoro. In questo esempio, uno spostamento assiale di 1 µm provoca un aumento della forza assiale di 6,9 N e una riduzione del momento torcente attorno all’asse z di 0,1 Nm. Poiché il cuscinetto in questo caso è soggetto esclusivamente a un carico radiale, non si verifica alcun accoppiamento tra le componenti radiali e assiali. Questa situazione è diversa quando sono presenti contemporaneamente carichi radiali e assiali .
I seguenti diagrammi mostrano la forza radiale e il secondo elemento diagonale principale della matrice di rigidezza tangente in funzione dello spostamento radiale di un 6204-C3, per due diversi valori di spostamento assiale.
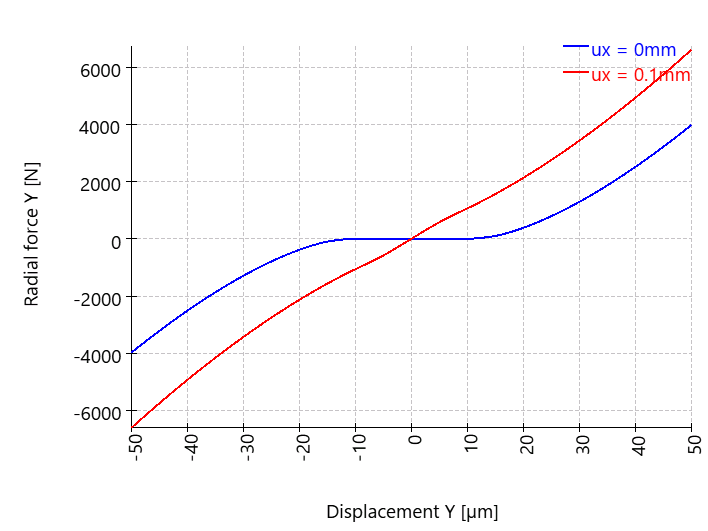
Forza radiale in funzione dello spostamento radiale per due valori di spostamento assiale
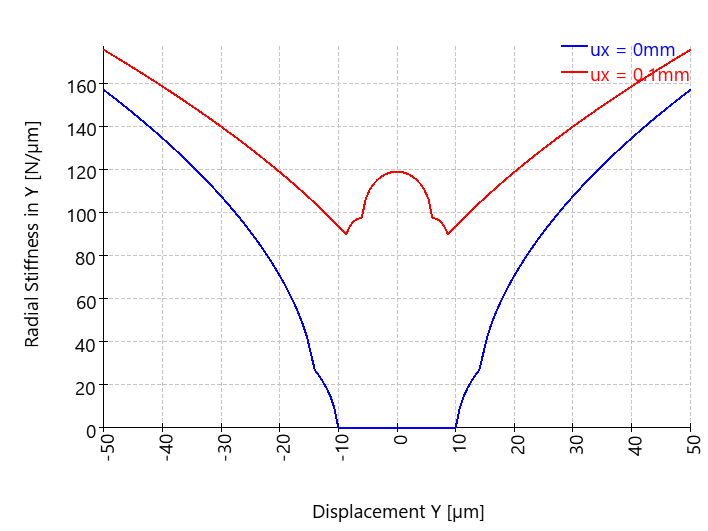
Rigidezza radiale in funzione dello spostamento radiale per due valori di spostamento assiale
Poiché il cuscinetto a sfere radiali presenta gioco, la forza radiale e anche la rigidezza radiale risultano in parte nulle. Si osserva che il modello semplificato basato su forza = rigidezza × spostamento non è valido per cuscinetti volventi non lineari. Il punto finale della curva blu è significativamente inferiore a 7750 N (ossia 155 × 50), e anche il punto finale della curva rossa è inferiore a 8750 N (175 × 50). La causa di questa discrepanza è da ricondurre alla non linearità della rigidezza del cuscinetto.
L’andamento forza-spostamento del cuscinetto può essere descritto tramite la matrice di rigidezza tangente K nel modo seguente:
F(u) = F(u0) + K*(u-u0) = F0 + K*u – K*u0 = K*u + (F0 – K*u0)
Per ottenere la corretta deformazione statica in un calcolo FEM, non è sufficiente considerare solo la matrice di rigidezza tangente: è necessario includere anche il vettore di forza (F0 – K*u0) per tener conto della non linearità.
Nel caso di una rigidezza lineare, questo vettore di forza è pari a zero.
Se si vogliono calcolare solo le frequenze proprie, senza una soluzione statica, il vettore di forza può essere omesso. Tuttavia, per ottenere una soluzione statica corretta, questo termine è necessario.


